

Consider information,
trust, fairness, reciprocity and the sequence of moves.
In orser to make the question easier I am going to assume that there are only two individuals in our model, Mr1 and Miss2, and only two commodoties, x and y. Both of the persons have an initial endowment of x and y, the total number of goods in the economy is their sum. As people can trade the final outcome always lies in the so called Edgeworth box:
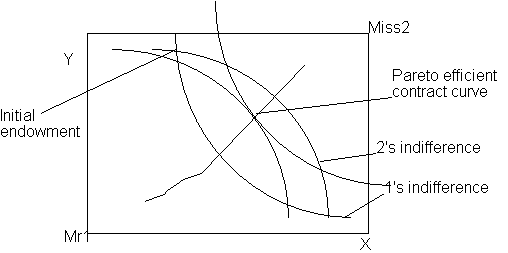
Indifference curves can be drawn from their initial endowment. It is clear that when bargaining occurs the final outcome will lie inside the "lens" as only then are both parties made better off. Pareto efficient is the outcome where none of the parties can be made better off without making the other one worse off, so at that locus the indiference curves must be tangential. It is noted of the graph as the contract curve, it is reached when individuals are rational (ie nobody worse off after agreement) and efficient. The same situation can also be represented by utility diagram, measuring people's utilities on its axis:
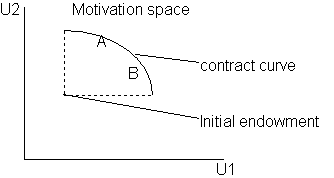
But none of the theory actually tells us where exactly on the contract curve is the final outcome. Person 2 wants to be more on A and person 2 on B and where they exactly going to end up depends on their relative bargaining strength. If they do not reach an agreement at all, then they will be both worse off.
So they must bargain. In real world there are legal and physical laws to constrain the choice. There are three general instruments that help to sustain "agreement": law, social norm and moral code. Also the final outcome depends very much on how much people will value the thing after a time period. If they are bargaining over a thing whose value diminishes with time they are more likely to do much looser offers in order to reach the agreement very quickly. On the other hand if the value of the asset rises over time (for example like computers are getting cheaper) people will not rush to buy them, they know there is going to be a better offer for both of them, although they cannot use the thing meanwhile.
It would be too complicated to deal with infinite numbers of possible outcomes, so I limit myself to two people and two outcomes. They are said to be involved in a game, with rewards shown in a fllowing game matrix:
|
1\2 |
a |
b |
|
a |
15 15 |
0 20 |
|
b |
20 0 |
10 10 |
That means, assuming that they play simultaneously, that if 1st person chooses to do a and 2nd b then 1st would get 0 and second 20. If there is no way of enforcing the game then they will choose bb, as it is better for both of them to choose b whatever the other person chooses to do, b is their dominant stradegy. Game is said to have a Nash equilibrium at bb. As seen both of them would have been better of at choosing aa, but this does not happen without outside influences. This type of game is called the prisoners dilemma.
This equilibrium outcome is not cooperative, a cooperative outcome would be aa. So there three things that have been set up externaly in order for these people to reach an agreement of aa. They are law, social norm and moral code. So if people sign a contract there is a punishment for breaking it. If the punishment is say 40 units for choosing b then payoff matrix would be:
|
1\2 |
a |
b |
|
a |
15 15 |
0 -20 |
|
b |
-20 0 |
-30 -30 |
So it is obvious that the dominant stradgedy will be aa. There is however a problem with lawers fees. If they amount to more than 5 per person they are better of adopting a non-cooperative stratgedy instead. So it is sometimes more profitable not to cooperate than ensure that the other person is not free riding on you.
Moral code and social norms are there also to enforce people to keep the contract. For example if 1 promises to choose stradgedy a then if he doesn't feel at least 5 units worse if he breaks the contract, or the social punishment would not be greater than 5, then he will break the contract.
Now if the game is carried on in an envirronment without law, but infinite times, then the stradgedy that wins is tit-for-tat. That means people will soon realise that they are better off cooperating and will cooperate. However when they do cooperate then there is a temptation for one to stop cooperating and try to free ride on the other. That should not be allowed, so following one's defeat (choosing b), the other person should in the next round choose also b to punish 1. Now when 1 understands his mistake and chooses a again, 2 should be forgiving and choose a as well. This is the tit-for-tat stragedy. But people do not know that and problems arise when they are envious (want to earn more than the other and are thus both worse off), or try to be too clever and try to guess others stradgedy, because this is likely to be wrong, or leave the other player without punishment for defeating.
But if game is finnished after x number of turns, then on the last turn one is better of cheating as the other one cannot punish him. Now if the other one knows first is going to cheat on the last turn anyway he is going to cheat on the turn before, so again non-cooperative situation occurs and we need laws.
Another problem arises when there are more than one outcome. they canall be ebneficial to both of the players, but more beneficial to one of them. So the otherone becomes jelous. Or both players show in their offers that they actually receive a lot less utility from the equilibrium than they actually do. SO if the thing does not "spoil" with time they could continue on bargaining.
If it does spoil then a complex theory was developed by Rubinstein that said an agreement is reached in one turn. But this theory assumes perfect knowledge and says outcome will minimise the product of shortfalls from a reasonable maximum utility of both individuals. A theory was developed by Nash, but this only went as far as saying what will be the outcome after two moves. For example, if one is selling and the other one can only accept or reject the offer, and the thing does not have any value for the seller, and its value for the other one is either h or l, h>l, Probability(h)=q. Then with a single round seller (S) would compare l and q*h and offer it with a price that's expected income is higher. If it chooses to sell at h it has a chance of loosing altogether, if buyer (B) is the one that only buys at l! But if there are two moves then the first move of the S is to go for h and see if B accepts. Now even if B is willing to accept, he wount, as on the next round S is likely to think B is the one that only buys at l, and offer it with a lower price. The final outcome is very hard to find and there are different theories about it.
Oh, yes. Otherwise there would be no strikes. Union is basically wanting to get a higher wage by reducing companies profits. There is again a minimum profit that the company is prepared to accept (p0) and a minimum wage that the workers are prepared to accept (the wage they can go elsewhere, w0). Original situation occurs where MC=MR for firm and labour is paid its minimum wage:
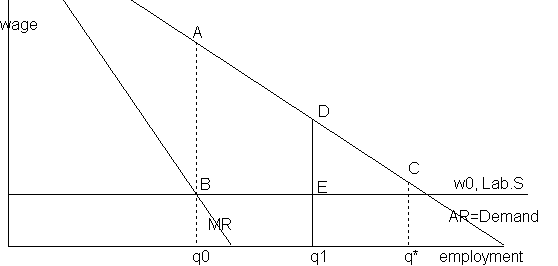
This graph shows the initial employment q0. Labour could have any empolyment and wage combination in ABC, lets say it chooses arbitarily q1, now it wants a wage D there, whereas employer wants to pay E at that point. So there will be a bargaining process. Again the longer they bargain the worser the outcome goes (as workers are on strike), so they might want to ask lawers or somebody to intermediate. Their contract curve is thus DE and no theory can yet unambiguously say where they are going to end up.