Custom Search
i) This work is about different growth models (Solow, Ramsey and endogenous technology and human capital models in New Growth theory).
ii) Empirical success usually evaluated by how well it fits stylised facts.
iii) Economic growth as a bad proxy for welfare? Inequality, sustainability should also be included. I will not talk about this issue.
iv) Fluctuations their behaviour and effect on welfare. However, short run fluctuations unimportant to long term welfare in this essay.
i) Model of the economy - Y=C+I, I=S, Y is GDP whose growth we are talking about. It generally grows over time.
ii) Saving ratio %age of income saved. Consumption cannot account for all of the increase in Y over time.
iii) We are talking about per capita Y
iv) Different models take different assumptions Solow assumes a production function and Ramsey individual optimisation (define them)
v) Stylised facts - differences in incomes across countries, speeds of convergence and determinants of growth (growth acting as a proxy for welfare) and answer question why have western economies suddenly grown.
i) Solow
(1) Setup
(a) Assume production function Y=f(K,AL) where A is technology assumed to affect only the effectiveness of labour. Constant returns to scale.(gains from specialisation exhausted)
(b) k=K/AL, Y=f(k) k is capital per unit of effective labour. Inada cond.
(c) Constant tech. progress and population growth dA/dt=gA, dL/dt=nL.
(d) Output divided between consumption and investment, constant depreciation d, and constant saving (=investment) s. dK/dt=sY-dK
(e) dk/dt=sf(k)-(n+g+d)k
(2) Implications and dynamics
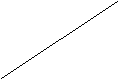
(a)
break even investment (to keep capital per unit of
effective labour constant
(n+g+d)k
In equilibrium dk/dt=0 at k* - balanced
growth path of Y at rate (n+d).
Actual investment sf(k)
I/AL
(b) Capital accumulation cannot account for large differences accross countries
(c) The interesting variable (technology, saving rate) is exogenous
(3) Saving rate
(a) Can change freely
(b) Increase increases the stable growth path level of k. Increase in the growth rate of Y is only temporary. However, the level of Y increases through multiplier. So only level effect not growth effect.
(c) Effect on consumption depends whether we are at golden rule capital level (f(k)=n+d). Normally countries are below, so s increase increases c.
(4) As individuals are not modelled, no welfare information.
(5) Empirical:
(a) Quantitative effects taking reasonable model (Cobb Douglas) and reasonable values (1/3 is capital. depreciation 5%) shows that saving rate changes have very little impact on final income. Thus saving rate differences cannot explain stylised facts. Romer and Weil show that to be consistent with data K/Y=0.6 not 0.3 as conventional. Solow model bad, see Human Capital models.
(b) K/Y ratio settles down in practice does not show any upward/downward trend. AL technology model might be right.
(c) Convergence too slow quantitatively. Convergence to conditional growth paths taking different s and n into account do countries converge? Baumol says yeah, for western countries. De Long shows that problems with sample selection and measurement error make this result invalid.
(d) Rates of return to account for differences, massive differences in rates of returns needed. Not in practice. (Fedelstein, Horioka). In open economies increase in s would be invested abroad, as rates of returns must be equal worldwide. In practice extra saving only invested domestically. Either Solow model bad (restrictions on capital mobility) or underlying forces affecting both S and I.
(e) Thus differences in A across countries must account for stylised facts, not s. Capital accumulation cannot account for cross-country differences or long run growth. However, technology can diffuse quite quickly empirically, thus does not support Solow.
ii) Ramsey
(1) Setup
(a) Capital stock and pop. still exogenous, due to household optimisation both K and s endogenous.
(b) Firms have pdf Y=F(K,AL) and max profits. They employ capital until
it earns its marginal product. When no depreciation r=f(k)
Labour earns marginal product too, real effective wage w/A=f(k)-kf(k)
(c) Individuals max U=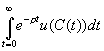
[
is instantaneous utility, CRRA, where θ is risk
aversion coefficient, ρ is discount rate] subject to discounted real wage
and capital income from savings and initial capital.
(d) Solving Lagrangean for household yields Euler equation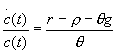 
where c=C/A. Meaning that C is increasing when real return
exceeds discount rate.
(e) Dynamics adding the constraint that households assets cannot be negative in the limit, economy reaches a saddle path equilibrium with stable c and k.
(2) Implications
(a) Very similar to Solow
(b) Saving is endogenous and depends on the risk aversion etc. thus we cannot look at the direct effects of the change in s.
(c) c is below golden rule c, because people value present small c more than future larger c. Thus increasing savings at present can create more c in the future.
(d) Welfare is maximised, as markets are competitive (Pareto cond. satisfied). However, this is due to infinitely lived households in Ramsey. Taking Diamond overlapping generations model can result in dynamic inefficiency as people save too much for old age. Central planner by using pay as you go mechanisms can increase welfare (basically k goes above golden rule level). Pareto condition of finite number of agents is not satisfied here.
(e)
A C B c dc1/dt=0 dc2/dt=0 saddle path dk/dt=0 k
Discount rate fall
effect is similar to s rate rise in Solow
Economy goes A to B to C because k cannot move instantly.
(3) Empirical
(a) Quantitative effects
(i) Speed of adjustment taking rho=4%, n=2%, g=1% and theeta=1 implies s=20% and the growth rate towards equilibrium is 5.4%, (Solow was only 2%). Thus more realistic, due to the fact that saving increases when k is below its long run value (due to interest rate increase and intertemporal substitution).
(b) Bond or tax finance and the Ricardian Equivalence. RE holds in Ramsey model. Empirically increased taxes increase total saving. Ramsey model should be extended to include liquidity constraints, non-lump sum taxes, and rule of thumb consumption.
iii) New Growth endogenous technological process (R&D models)
(1) Setup
(a) R&D sector with conventional pdf.
(b) However, R&D does not have constant returns (duplicating the world leads to the same discovery again, that is worthless)
(c) Assume for the economy Y=f(K,AL) and A=BK (learning by doing). K enters twice, taking the simplest form for f(.) Y=AK gives a linear growth model.
(d) dK/dt=sAK steadily growing K.
(2) Implications
(a) Long run growth is endogenous and depends on s. Increase in s leads to a permanent increase in the growth rate of Y.
(b) One can include learning by doing to Ramsey, in which case, increase in discount rate, leads to increase in s, and permanent increase in the growth of Y
(c) Many market imperfections:
(i) technology is nonrival, non-excludable and R&D itself when produced leads to further R&D. Thus too little is produced in a competitive economy. Saving more to technology can improve welfare
(ii) The first one to invent the technology gets the patent. Too much saved in technology then (business stealing)
(iii) Overall implications for government policy ambiguous.
(3) Empirical:
(a) Quantitative: Lags in technological division to account for cross-country differences must be a century. Too long, thus AK cannot account for Cross country differences. Thus hard to test empirical effects of s.
iv) New Growth theory of Human Capital
(1) Setup
(a) Resembles Solow, with higher capital ratio
(2) Implications
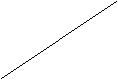
(a) k1* k2* k s2f(k) s1f(k) (n+g+d)k (n+g+d)k s2f(k) s1f(k) k1* k2* k Solow Human
Capital
In Human capital
models changes in s lead to much larger changes in steady state value of k*.
(3) Empirical issues
(a) Quantitative changes in s need not to be extraordinary to cause the changes in Y that are observed worldwide.
(b) Mankiw Romer when capital share is 0.7 the differences in saving rates can account for the differences in the Y.
(c) Conditional covergence was also tested by Mankiw with less success
i) There are hundreds of models, and still all are too gross simplifications. However, even though some of the New Growth ones fit the empirical results remarkably well.
ii) The predictive power is weak, and the saving rate is not essential to either welfare or growth.
iii) Saving in broader concept to human capital can be very relevant but is hard to test. It is very hard to measure the quality of education, but the quantity is a bad proxy.