Custom Search
A method of modeling expectations that captures the ability of human beings to adapt to their environment was suggested in 1960-s. The notation of rational expectations, was introduced into macroeconomics in 1972 by Robert Lucas and it has since become standard as a way of treating expectations. Rational expectations essentially assume that the beliefs of workers and firms will be right on average. Rational expectations means that the expected price is chosen in such a way that, given the ex post distribution of shocks, sometimes the observed price will turn out to be higher than expected and sometimes it will turn out to be lower. However, on average people must be correct in their expectations. Some random deviations are permitted, however, as soon as there is a systematic component in the deviations, people will change their expectations. This will lead to 2 important conclusions. Firstly, if people suddenly believe in something and start acting in a way that should bring the belief about, then the belief comes true. Secondly, people cannot be systematically fooled. Thus the beliefs will depend on the policy pursued by the government as well, because otherwise the government could systematically fool people. According to rational expectations, as soon as the government changes its policy openly, the people will change their expectations as to offset any distortions to the equilibrium. Only unexpected policies can shift the economy out of equilibrium temporarily. Here lies the main prediction for the effectiveness of economic policy.
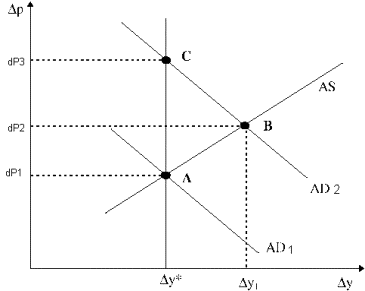In the 1960’s the Phillips curve was widely
perceived as a policy “trade off” that could be exploited by a benevolent
policy maker who chooses between inflation and employment. According to this
point of view, the government could stimulate employment and growth by
increasing the rate of money growth. However a policy of pursuing high economic
growth would have its costs in higher inflation rate. In effect, the government
would be picking a point on the modern Phillips curve such as point B, that was
to the northeast of its intersection with the natural rate, at A. This idea is
illustrated in this figure. It shows the Philips curve AS as being the
relationship between the change in prices (dP1) and change in output (dY*).
This Phillips curve would hold if households and firms expected the inflation
rate dY*. This expectation is rational only if the average aggregate demand
curve is given by AD1; the position of AD1 is determined by the average value
of money supply growth. The actual aggregate demand curve in any state of
nature is different from AD1 because of money growth shock. Some economists
argued, in the 1960’s, that it would be possible to raise the average rate of
money growth thereby shifting the aggregate demand curve to AD2. If expected
inflation were to remain at dP1 then the intersection of the average aggregate
demand and average aggregate supply curves would occur at point B. The realized
inflation rate would, on average, equal dP2. However, then people would be
making systematic mistakes. Rational expectations predict that the aggregate
demand can shift to AD2, but it will not lead to output dY1. Instead, inflation
will increase to dP3. This happens because people expect prices to grow at an
accelerating rate and thus require the payments to accelerate even faster,
until the natural rate of equilibrium is obtained again.
So the fiscal policy is ineffective in smoothening out cycles and expanding employment, as long as it is predictable. Thus some writers have argued that there is no scope for demand management at all. This result, however, depends crucially on the model we use. In the current simple model that is indeed the case. However, in a different model rational expectations might actually help fiscal policy. For example, where people expect the expansionary fiscal policy to bring about increased economic activity, they will increase their economic activity as well, because they will anticipate the increase in demand. The result is greatly increased output, not just prices.
Returning to our classical model, the ineffectiveness of the fiscal policy also tells something about the financing. In particular, it predicts that there should be no difference in the outcome whether the government deficit is financed out of taxation or out of monetary expansion (issuing of bonds). This is because government cannot borrow forever, and has to repay its debts at some point. And the repayment will be made out of increased taxation in the future (in the closed economy). Thus, when government increases PSBR, rational individuals will start saving for the future increases in taxes. This fact is empirically proven – government increased borrowing is usually matched by increased savings. Similarly, in the open economy the repayment can be made by selling country’s assets to foreign institutions. However, this will again result in less revenues for the government in the future, and ultimately higher taxes. Thus it should not matter for the economic activity how the government finances its-self. Monetary financing would only fuel inflation, so it should be avoided.
There are obviously numerous criticisms for this analysis. Most obvious of them being that the people could pass away before the increased taxes. If they know that, they should not care, and will spend more as a response to tax cut. However, bequests must also be included to this model. Using the household instead of an individual would create an institution with unlimited lifetime (because the money is forwarded as bequests), so the increased saving would still occur.
This is about the only real empirical evidence the rational expectation offers. By its nature, it tells that the empirical evidence should not just depend on the real variables of the economy (inflation, unemployment etc), but also on people’s predictions. So it explains why current models fail to give good predictions (i.e. why Philips curve shifts etc.). However, the theory of how the rational predictions are formed is still very young and inaccurate. Thus the theory can explain the past quite well (by just incorporating the change in expectations to points where the data changes). However, its predictive powers are weak.