Custom Search
Keynes thought he was one equation short – having three variables and 2 equations. He tried holding the price level, or the wage increases, constant. This led to spiraling inflation. Neoclassical economists tried to hold the national income constant at its full employment level. That led to increasing “natural levels” of unemployment during the 70-s. To me, it seems that the modern endogenous growth models are trying the third option – to keep the interest rate constant. It helps to think in these terms when I evaluate the importance of savings in modern growth theories. Because ultimately one wants to know whether indeed the theory just restricts one variable, in order to make sense, or whether there is something more substantial, maybe even a third equation, involved.
But before I express my understanding of the modern growth theory, a bit about the history of economic thought just to answer the question.
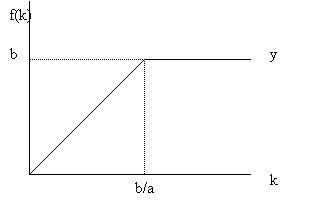
Firstly about the Harrod-Domar growth model, which is the oldest of the three. As all the models here presented crucially depend on their assumptions, I shall start by mentioning that Harrod-Domar model uses the Leontief’s production model. It says that the output, which is also the income in a closed economy, depends on the factor that is in shortage. Y=Min(aK,bL) where a and b are constants.
When there is not enough capital, unemployment will occur, and when there is
not enough labour, some machines will lie idle. That means capital and labor
cannot be substituted instead of each other. Now if we divide both sides by the
amount of labor L and define k=K/L – ie the capital to labor ratio, and y as
GDP per capita, we get a new equation:
y=min(ak,b). Increase k up to b/a will lead to increases in output as more
people are employed. After that however, output will not increase. Graphically:
The fundamental dynamic equation of the capital stock says that in a closed economy
dk/dt=s*f(k)-(n+q)*k (i)
That means the capital/labor ratio grows with investment, minus the depreciation of capital and the growth of work force. Investment = Savings in a closed system, and all models assume that a constant amount of income is saved (marginal propensity to save, s), so the investment is the proportion times income. n is the growth of labor force and q is the capital depreciation. For the dynamic stability dk/dt must equal 0 – the capital to labor ratio must be constant. As in Harrod model a and b are constants and represent exogenous technology changes, the only thing that chnages income is the capital labor ratio. For equilibrium we must have s*f(k)/k=n+q (from i).
Or graphically:
sA n-q Sf(k)/k B/a k* k sA n-q Sf(k)/k B/a k
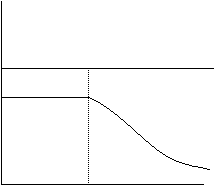
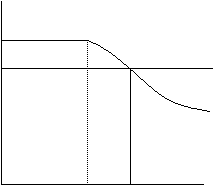
In this case, when savings are not big enough to cover make dk/dt=0. So there is no positive steady state value, sk/dt is always negative, meaning that the economy shrinks in real terms and has rising unemployment. The right hand graph depicts the case where s is too large – economy has exceeded the optimal amount of capital (when ratio is b/a) and has some lying idle. But as the labor quantity grows at rate n, so does the number of machines lying idle.
This is a pretty bad picture. The full employment with no idle resources occurs
only when sa=n-q (sorry about the capitalization, word7 thinks letters at the
beginning of sentences should be capitals J ). Thus savings has a
very important role to play, it must exactly mach (n-q)/a for the capitalist
system to work. This is the razor-edge model, and it has been argued that
government should have the role of balancing the terms in order for the society
to function properly. But of course the assumption of no capital-labor
substitutability is unrealistic, as is exogenous saving rate (people are
assumed to continue saving, although there are some machines idle!).
A bit better model, devised in 60-s, uses Cobb-Douglas production model. All else is the same. This is the neoclassical model. In this case
y=akb where b is a constant 0<b<1. The steady state will be:
When the saving is at s*, the national income will be at its
optimum. When saving falls then the steady state value for k falls, and thus
income will fall. Similarly when saving exceeds the optimal value the national
income will be higher, however, the consumption will be lower than in k* case.
But as economists are more concerned with consumption than national income, the
higher state will not be preferable. The whole theory about the optimal level
of savings in this case is the golden rule of savings theory. However, as it is
so out of date, I won’t go into any greater detail than that (its to do with
tangents of f(k) curve and all that).
Finally the endogenous growth models were invented to take the technological change into account. One example is when there are no diminishing returns to capital – the AK model. It is a reasonable assumption when one counts the human capital as well. In this case Y=AK. A is still a constant technology parameter, but it is assumed that as K increases, there are enough technical spillovers to keep the rate of increase of K the same – technical innovations will offset the diminishing returns on capital.
In this case saving will not have a role to play as the parameter determining the final equilibrium steady state. It will instead determine the growth rate of Y, because the growth rate of Y depends on the growth rate of K that in turn, through the fundamental dynamic equation depends on s.
Similar results are obtained when one uses CES model – the hybrid of Cobb-Douglas (where there is perfect factor substitutability) and Leontief (no substitutability). In this case there are diminishing returns to capital, but only to a certain extent. Savings determine that extent and thus again determine the ultimate growth rate of economy.
Using CES leads to the empirical result that the growth rate and absolute income levels of similar countries are inversely related. Intuitively, when a country has a high national income, then it would use much new technology. However, this technology will be absorbed by the neighbor nations, making their economies grow faster and ultimately converge. However, when 2 countries have different savings ratios (or population growth or depreciation rates etc) the GDP-s will never converge completely. It might be wise then for the countries that lag behind to artificially increase the savings rate.