

There are two types of consumption theory. One predicts the consumption out of income. It was first popularised by Keynes and later on extended by Modigliani and Friedman. It is what is now known as permanent lifetime hypotheses. It has been able to predict the longer-term consumption, however, it cannot pick up the year by year variance in consumption. Furthermore, it could not predict the fall of the savings ratio in 80-s.
The second theory, so called Euler’s equation, has risen out of the work of Hall. The original paper argued that there is no way one can predict consumption (the series is non-stationary, or follows a random walk), but extensions to that theory do allow for predictions. The theory usually assumes rational expectation and thus says that current consumption depends on all available past information. This theory is very good in picking up year to year variations in consumption. However, it is harder to make any long-term predictions based on that.
Usually the two theories are taken together. Writers then show how certain modifications (inflation, increased income variability etc.) change these two models. However, in this essay I will try to talk about the two theories separately. It will cause some overlapping, but I think it is a lot clearer.
The Keynesian model takes consumption as a fixed proportion of
current income. C=a+bY. One can extend that to say that the function is
exponential instead(C=aYb), and use the logarithmic form instead. It
is quite a good first approximation, when the economy is stable. However, the
relationship broke down during the 1970-s.
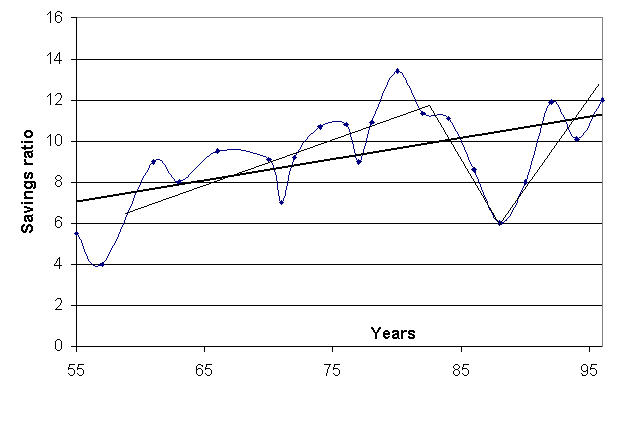
The curved line is the actual ratio, the bold line is the prediction that shows a constantly increasing savings ratio as the income increases (savings ratio is S/Y, C+S=Y in a simple Keynesian framework, thus this is the direct outcome of the C=a+bY model). Before getting into the reasons why the consumption should be a proportion of income, one can see straight away that the doted line is a much better approximation, showing a structural break in the late 70-s.
Keynes did not provide much theoretical reasoning, why C depends on Y. He said that the saving is income forgone, thus it must yield more income in the future. One gets interest on their savings. When the interest rate is higher than the discount rate (the rate that people value future consumption less than current) then people save and vice versa. However, the discount rate depends on the actual amount of consumption. Modigliani (PIH) and Friedman (Life Cycle) suggested then that the utility maximising agent would want to smooth out their consumption pattern dissaving when income is low and saving when it is high. The aggregate amount of savings, however, depends on the utility that the actual saving process brings (otherwise there would be 0 savings on aggregate – people with low incomes would dissave exactly as much as people on high income periods would save).
This utility comes in several forms. Savings bring profits as interest and it also guards against unexpected shocks in income. Thus it acts as a buffer. However, for statistical reasons, the differentiating between these types is unimportant.
What statistically matters is how one measures the permanent income. The simplest measure is to take the past incomes as a proxy for ones permanent income. One should obviously put more value on the latest income figures. Thus when there is a sudden increase in income, first people will think is a fluke and only alter their consumption by a tiny amount. They save the rest, so that this tiny increase in consumption could be sustained forever, after the income has return to "normal". However when the income change is permanent people will readjust their permanent consumption forever. This is the transitionary income effect on savings and it makes the statistics much more consistent with the data. This is also the basis for Euler equation form of the consumption, which I will talk about later.
On average then, people should not make mistakes about their income prediction. They should be able to deduce their total earnings over their lifetime, divide that by the number of years they live, and consume that amount every year. The rest of the income is saved then, or when the income is not sufficient, savings are used up. However, this theory predicts the total amount of savings stock, not the additions to that stock. When there are no bequests and everything in the economy is stable, then the stock of savings should be stable and thus no aggregate savings occur. Aggregate savings only occur when the conditions change, because then there are more people saving than using up savings, or vice versa.
One of the conditions that can change is the income. When income rises in general, there are more people with higher lifetime consumption expectancy. But these people are by definition working. Thus in the part of their lives when they save. The pensioners will not change their consumption patterns, because they do not work anymore. When the working people realise that they can have higher consumption all through their life, they will obviously save more to account for their retirement. This is mostly why we observe a relation between income and savings. And because incomes have risen in general over the years, we have seen an increase in savings with the savings rate remaining fairly stable.
Other things that can change include the credit restrictions and population composition. It can be argued, that the general increase in savings rate is caused partly by the increasing life expectancy (people will have to save for longer periods), and that the fall in savings in 80-s was caused by liberalisation of credit aided by the reduction in the variability of income. The second proposition needs a bit clearing. Firstly, because of income variability and credit restrictions, the optimum lifetime consumption is not a straight line, but more of a hump shape. This occurs because people cannot borrow as much when they need to when they are younger, because banks will not give them credit. Similarly, everyone saves a bit more than optimal to take account for the rainy days. Thus the income and consumption looks like:
|
|
Dissaving Saving |
Now it is clear that when credit restrictions are eased, the only people that are concerned with that are the ones who like to borrow. When they do so the savings rate will fall and the consumption function will become more of a straight line.
Similarly the precautionary motive for saving diminishes when income variability falls. However, throughout the precautionary motive enters another important factor that predicts savings – it is the inflation rate. When inflation rises the real interest falls and thus people will have an incentive to save less. However, in general the nominal interest is raised when inflation occurs leaving the real interest constant. In this case it was observed that the savings actually increase. This happens because the real value of the savings is eroded by the inflation. Thus people have to save more to keep their necessary precautionary buffer of savings.
Finally, the asset prices, or income from property, also affect the solved-out model as well as the Euler version of the equation. The effects enter mainly through the rate of interest and stock market prices. In simple classical model the interest rate is positively correlated with savings. And even in Keynesian model interest rate affects savings through money demand and money supply (Ms change has impact on savings through the national income). Thus when interest rate increases savings should increase. However, empirically it is not that simple because interest rate changes have income effects as well as substitution ones. But more about that later.
There are also number of smaller modifications to the model that I will not go into much detail at present. For example the way one takes bequests into account matters for one's s saving decisions. Also the tastes of people can change etc. However, these are not easy to express empirically.
Since rational expectations, the emphasis has shifted from the solved out approach to Euler equation of consumption. In its original formulation by Hall it said that consumption cannot be predicted, that it follows a random walk described by the equation:
Ct=Ct-1+et
Where et is a random error term with mean 0. As this is a non-stochastic equation consumption cannot be predicted.
This equation has caused much recent research into the field, with the outcome that it is wrong. There are some explanatory variables that can predict the Ct other than the consumption of the previous period. But this is a rejection of the rational hypothesis – if people would be entirely rational, and would want to smooth out their consumption functions, then they would use for their current consumption everything that was known the period before (represented by Ct-1 term) plus all information that becomes known in the period t. But this new information should be random. However, it is reasonable to assume that the econometricans will find the information out before the public. Thus it is not surprising that the movements in stock market can predict consumption. Stock markets consist of professionals that know information better and before than the average person. Thus stock market serves at present as an indicator for current consumption. When it rises, people will have more assets and are likely going to consume more after a while. I said it predicts it at present, because as more models use the stock market, people will become aquatinted to that and will start using stock market data as well. Thus the relationship can break down in the near future.
There are also further indicators, whose predictive power is not that great. Furthermore it varies from country to country, with unemployment, for example, being a predictor in Australia, but not in USA. Further predictions (to name just a few that have been tested) include the inflation rate, interest rates, liquidity constraint changes, the change in the composition of durables in the basket of goods (especially the extra cost of altering their composition), and the relative preference to leisure (ie whether consumption and leisure are complementary goods or substitutes).
But the main reason these predictors are used is the strange phenomenon that the consumption is oversensitive to changes in income. Small changes in income will bring about large changes in consumption for some reason. According to the PIH, the transitionary income is saved, however, in reality people actually consume most of the transitionary income. This is the reason for much research into basic Euler equation.
There are many criticisms to Euler that Muellenbauer has brought out nicely. The main one is that it is very hard to use the Euler equation for any longer predictions, because the main item in it will be the previous consumption. Thus to predict consumption 5 periods in advance, one would need 5 equations nested inside each other. Errors are likely going to multiply, and the computation involved is huge. There are also numerous theoretical problems that will arise. It is not clear how one should model the representative consumer (ie whether they can substitute perfectly between leisure and work etc.) Also there is obviously strong correlation present between the variables and the direction of causation is also hard to explain (it is not clear, for example, whether a fall in consumption causes a rise in unemployment or vice versa).
As seen, there are 2 theories to consumption. However, they are not entirely competing ones, more like complementary. One should not worry about the PIH, when the likely consumption for the next year is needed. However, Euler equation should not be used for estimating the effects of a pension reform in 20 years.