In a two good two person exchange economy, use offer curves and an Edgeworth Box analysis to

1.      demonstrate that any Walrasian competitive equilibrium is an element of the core

The core in the two person economy is the contract curve. It is the set of allocation having the property that no person can be made better of voluntarily (i.e. without making anybody else worse off. It is depicted in this diagram:

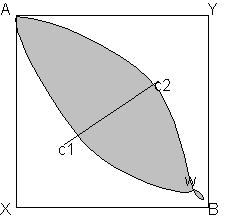
For now we take 2 goods A and B and two individuals X and Y.

There are also 2 consumers with utility functions U_y­=f_y(A_y,B_y), and U_x=f_x(A_x,B_x) ddepicted as the convex lines. Endowment is at w. It is clear, that every point outside the shaded lens is preffered less by one player, than the initial endowment. However, improvement can also be made on every other point, other than the core c1 c2 where the indifference curves are exactly tangent.

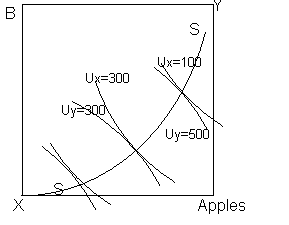
Core here is S-S.

Similarly core can be looked as the intersection of two persons offer curves. Offer curves are derived when offering a different relative price to the individual, and letting him go to the highest indifference curve. Offer curve is then the locus of this point (where indifference curve is tangent to the relative price line going through the initial endowment). There is only one relative price for which both individuals are willing to offer exactly opposite amounts (negative&positive). Thats the core.

A point of Walrasian equilibrium that lies in the core must have 0 exess demands on every good (otherwise people would preffer the other point). So if we map a normalised set of price vectors through the excess demand equation to excess demand vectors, there must exist a P that gets mapped to 0,0. As the prices are assumed to be continuos, the excess demand function must also be continuos.

OK, on normalised prices, the prices lie on a line from 0,1 to 1,0. These points get mapped to the Y axees and the X axees on the Z space becasue of the Walraz law. This states that p1z1+p2z2=0, thus if p1=0 z2=0 etc. As prices are always positive, the z2 and z1 must have an opposite sign for the Walras law to hold. Thus the function lies in the 2^nd and 4^th quadrant only, as it is continuos it must pass through the origin, which is the equilibrium point.

2.      derive an excess demand function for one commodity

Let the price of this commodity, x, be p. The gross supply is xi for the ith firm, and the gross demand is xh for the hth household. Summing over i and h respectively, we get aggregate gross supplys and demands of the good x. But the demand and supply of the good x depend also on all the prices of other goods, thus

Xi=Si(p1,p2,..,pn)

Xd=Di(p1,p2,..,pn)

 

Excess demand(e=Demand-Supply=∑xh-∑xi=Zx(p1,p2,...,pn)

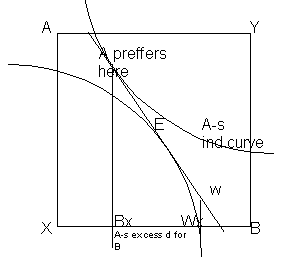
Excess demand is thus also a person X gross demand for a product B minus the wealth obtained when selling that product.

e_X^B=Bx-Wx

3.      show that Walras law and Walras equilibrium are two separate concepts

Walras law is an identity that always holds. Using the consept of excess demand developed earlier, the person X budget constraint is

P1Ex+P2Ex=0

As this applies to every person, you can just add them together and still get an answer of 0. Thats the walras law.

Walras equilibrium requires system to be in equilibrium. It is the set of prices where the demand is equal to supply and everybody gets their best possible thing (at the given prices given endowments). Its basically the core.

4.      demonstrate that there can be any odd number of Walrasian equilibrium but that even numbers are extremely unlikely

Excess demand function is has generally negative slope. It can ossilate in the middle, but it derivative is negative at the extremes. When it ocillates, it can give rise to multiple equilibria, but even numbers only occur when the curve becomes tangent. That is unlikely.

5.      how important is the assumption of convex indifference curves to the existence of a competitive equilibrium

It is not important when there are many small individuals. However, it is important for larger individuals, as otherwise discontinuities in demand will exist. Basically, Indifference curves will not necessary be tangent anymore at the same relative price for two consumers.

State and justify the two fundamental theorems of welfare economics.

1^st In equilibrium a competitive market must be pareto efficient.

The proof is by simple contradiction – people cannot afford more when they are in equilibrium in competitive market, thus they cannot be mafe better of.

2^nd theorem is the other way round. When aggregate indifference curves are convex, then any Walrasian equilibrium is pareto efficient. Proof could again be reproduced from anywhere really.